ضریب همبستگی پیرسون (Pearson correlation coefficient) یک روش آماری پارامتریک است که برای سنجش شدت و جهت رابطه بین دو متغیر استفاده می‌شود. این روش، همانند سایر روش‌های همبستگی، به بررسی روابط بین متغیرها به صورت دو به دو می‌پردازد. یعنی در صورتی که رابطه بین دو متغیر A و B را با حضور یا بدون حضور متغیری مانند C ارزیابی کنیم، همچنان میزان این رابطه یکسان به دست می‌آید. این روش که توسط کارل پیرسون (Karl Pearson) بر اساس ایدهٔ اولیهٔ فرانسیس گالتون (Sir Francis Galton) تدوین شد، مبتنی بر مفروضات آمار پارامتریک است.
هنگامی که می‌خواهیم همبستگی بین دو متغیر را که هر دو در مقیاس نسبی یا فاصله‌ای قرار دارند بررسی کنیم، از ضریب همبستگی پیرسون استفاده می‌کنیم. در صورتی که ضریب همبستگی جامعه ρ و ضریب همبستگی نمونه‌ای به حجم n از جامعه r باشد، ممکن است r به صورت تصادفی و اتفاقی به دست آمده باشد.
برای این منظور، آزمون معنی‌داری ضریب همبستگی مورد استفاده قرار می‌گیرد. با استفاده از این آزمون، بررسی می‌کنیم که آیا دو متغیر تصادفی و مستقل هستند یا خیر. به بیان دیگر، بررسی می‌کنیم که آیا ضریب همبستگی جامعه صفر است یا خیر.راین ضریب میزان همبستگی بین دو متغیر فاصله‌ای یا نسبی را محاسبه می‌کند که مقدار آن بین ۱+ و ۱- متغیر است. در صورتی که مقدار به دست آمده مثبت باشد، به این معنی است که تغییرات دو متغیر به صورت هم جهت اتفاق می‌افتد.
به عبارت دیگر، با افزایش در هر متغیر، متغیر دیگر نیز افزایش می‌یابد. در مقابل، اگر مقدار r منفی شد، به این معنی است که دو متغیر در جهت عکس هم عمل می‌کنند. به عبارت دیگر، با افزایش مقدار یک متغیر، مقادیر متغیر دیگر کاهش می‌یابد و بر عکس. از سوی دیگر، اگر مقدار به دست آمده صفر باشد، نشان می‌دهد که هیچ رابطه‌ای بین دو متغیر وجود ندارد و اگر ۱+ باشد، همبستگی مثبت کامل و اگر ۱- باشد، همبستگی کامل و منفی است.
محاسبه ضریب همبستگی پیرسون
ضریب همبستگی پیرسون میان دو متغیر تصادفی برابر با کوواریانس آنها تقسیم بر انحراف معیار آنها تعریف می‌شود. در مورد یک جامعهٔ آماری، ضریب همبستگی جامعه به صورت زیر تعریف می‌شود:
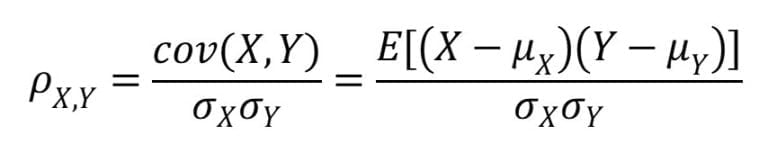
که در این معادله، cov کوواریانس، σx انحراف معیار متغیر X، µx میانگین متغیر X و E امید ریاضی است. امید ریاضی به معنای مقدار انتظاریست از یک متغیر تصادفی گسسته که این مقدار برابر با مجموع حاصل احتمال هر یک از پیشامدهای ممکن در مقدار مربوط به آن پیشامد است.
برای یک نمونه آماری شامل n زوج داده (Xi, Yi)، ضریب همبستگی پیرسون به شکل زیر تعریف می‌شود:
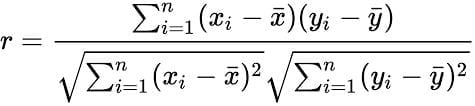
فرمول زیر نیز معادل تعریف فوق است:
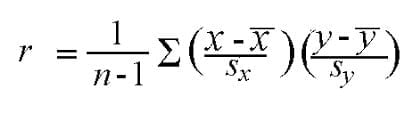
که در آن، کمیت‌ها به شکل زیر تعریف شده‌اند:
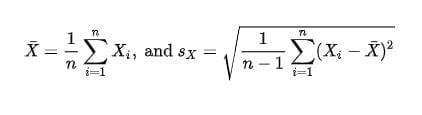
همان طور که پیش از این گفته شد، ضریب همبستگی پیرسون بین -1 و 1 تغییر می‌کند. اگر r=1 باشد، این موضوع نشان‌دهنده یک رابطه مستقیم و کامل بین دو متغیر است. رابطه مستقیم یا مثبت به این معناست که افزایش یا کاهش در یکی از متغیرها، افزایش یا کاهش مشابهی در متغیر دیگر ایجاد می‌کند.
در صورتی که r= -1 باشد، آن گاه رابطه معکوس کاملی بین دو متغیر وجود دارد. رابطه معکوس یا منفی حاکی از آن است که اگر یک متغیر افزایش یابد، متغیر دیگر کاهش می‌یابد و بر عکس. زمانی که ضریب همبستگی برابر صفر باشد، حاکی از آن است که بین دو متغیر رابطه خطی وجود ندارد.
چند نکته مهم در مورد ضریب همبستگی پیرسون
- صفر بودن ضریب همبستگی تنها نشان دهنده عدم وجود رابطه خطی بین دو متغیر است اما نمی‌تواند مستقل بودن دو متغیر را نیز نشان دهد. زمانی که ضریب همبستگی پیرسون بین دو متغیر برابر با صفر باشد، این متغیرها فقط در صورتی مستقل از یکدیگر هستند که توزیع متغیرها نرمال باشد.
- همبستگی بین دو متغیر تنها نشان می‌دهد که افزایش یا کاهش یک متغیر چه تاثیری بر افزایش یا کاهش متغیر دیگر دارد اما این همبستگی لزوما نشان دهنده رابطه عِلّی بین متغیرها نیست. برای مثال، اگر در یک مطالعه، قد و تحصیلات دو متغیر باشند که همبستگی مثبت قوی‌ای با یکدیگر دارند، نمی‌توانیم نتیجه بگیریم که افرادی با قد بلندتر حتما تحصیلات بیشتری دارند.
بنابراین، لازم است تا بین مفاهیم همبستگی و رابطه علّت و معلولی تفاوت قائل شویم. به عبارت دیگر، ممکن است دو متغیر همبستگی داشته باشند اما لازم نیست که یکی از متغیرها علت و دیگری معلول باشد. علاوه بر این، عوامل متعدد دیگری هم می‌توانند بر ضریب همبستگی اثر گذارند.
سخن پایانی
همان‌طور که گفته شد، ضریب همبستگی پیرسون یکی از ابزارهای مهم و کاربردی در آمار و تحلیل داده‌هاست که این امکان را به ما می‌دهد تا میزان ارتباط خطی بین دو متغیر را بسنجیم. این ضریب با مقادیر بین -1 و 1 تعریف می‌شود و نوع و شدت رابطه بین متغیرها را نشان می‌دهد.
استفاده از ضریب همبستگی پیرسون نه تنها در علوم آماری، بلکه در حوزه‌های دیگری از جمله اقتصاد، روانشناسی، علوم اجتماعی و بسیاری از رشته‌های دیگر نیز مورد استفاده قرار می‌گیرد. با این حال، همواره باید به این نکته توجه داشت که این ضریب فقط رابطه خطی بین متغیرها را بررسی می‌کند و در شرایطی که رابطه غیرخطی وجود دارد، ممکن است دقیق نباشد.
در پایان، باید گفت که شناخت و استفاده صحیح از ضریب همبستگی پیرسون به تحلیل‌گران کمک می‌کند تا با دقت بیشتری داده‌های خود را ارزیابی کنند و از اطلاعات حاصل از این تحلیل‌ها در تصمیم گیری‌ها و پژوهش‌های خود بهره ببرند.
