ضریب همبستگی چیست ؟ انواع ضرایب همبستگی کدامند و فرمول و نحوه محاسبه آنها به چه صورت است؟
در تحلیل‌های چند متغیره آماری، روش‌های گوناگون محاسباتی برای اندازه‌گیری وابستگی یا ارتباط بین دو متغیر تصادفی وجود دارند. منظور از ضریب همبستگی بین دو متغیر، قابلیت پیش‌بینی مقدار یکی از آن متغیرها بر اساس دیگری است. به عنوان مثال، عرضه و تقاضا دو پدیده وابسته به یکدیگر هستند. یکی از شیوه‌های نمایش ارتباط بین دو متغیر محاسبه کوواریانس (Covariance) و یا ضرایب همبستگی (Correlation Coefficient) بین آنها است.
هر چه مقدار این دو شاخص بیشتر باشد، نشان می‌دهد که ارتباط یا وابستگی بین دو متغیر بیشتر است. به عنوان مثال، می‌توانیم وابستگی بالایی بین دو متغیر میزان مصرف برق و دمای هوا را در نظر بگیریم چون هر چه دما افزایش یابد، استفاده از وسایل سرمایشی نیز افزایش داشته و مصرف برق بیشتر می‌شود. در نتیجه، وابستگی زیادی بین این دو متغیر دیده می‌شود.
با این حال، لازم است توجه داشته باشیم که کوواریانس یا همبستگی نشان دهنده ارتباط علت و معلولی نیستند، بلکه تنها معیاری برای نشان دادن میزان وابستگی بین دو متغیر محسوب می‌شوند.
ضریب همبستگی و کوواریانس
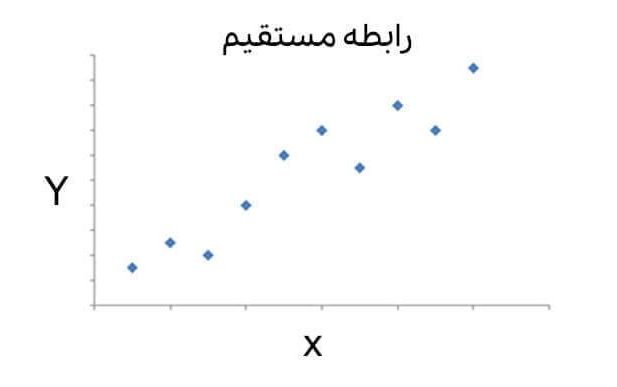
یکی از روش‌های نشان دادن ارتباط بین دو متغیر استفاده از کوواریانس (Covariance) است. این میزان جهت ارتباط بین دو متغیر را هم نشان می‌دهد. به بیان دیگر، در صورتی که مقدار کوواریانس مثبت شود، نشان می‌دهد که ارتباط مستقیمی بین دو متغیر وجود دارد. یعنی با افزایش یکی از آنها، دیگری نیز افزایش می‌یابد.
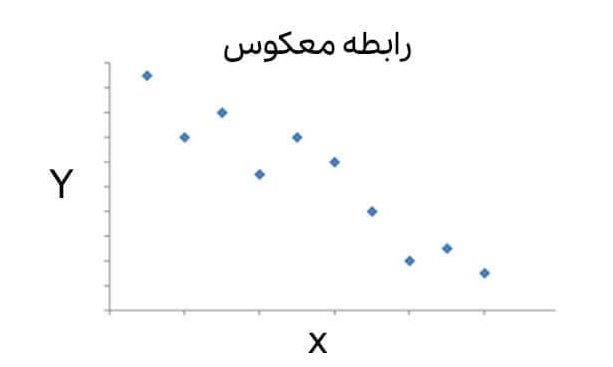
همچنین منفی بودن مقدار کوواریانس نشان می‌دهد که جهت تغییرات دو متغیر عکس یکدیگر است. به عبارت دیگر، ارتباط معکوس بین دو متغیر نشان می‌دهد که با افزایش یکی از آنها، دیگری کاهش می‌یابد.
در نظر بگیرید که X و Y دو متغیر تصادفی با امید ریاضی E(X) و E(Y) هستند. چگونگی محاسبه کوواریانس X و Y با رابطه زیر نشان داده شده است:
COV(X,Y) = E[(X – E(X))(Y – E(Y))]
ویژگی‌های کوواریانس
با در نظر گرفتن رابطه تعریف شده برای کوواریانس، می‌توانیم به ویژگی‌های آن به صورت زیر اشاره کنیم:
- تقارن: کوواریانس شاخصی متقارن است. به بیان دیگر COV(X,Y) = COV(Y,X)
- واحد ترکیبی: واحد اندازه‌گیری کوواریانس ترکیبی است. به عبارت دیگر، در صورتی که X با واحد متر و Y با واحد کیلوگرم اندازه‌گیری شده باشد، واحد اندازه‌گیری کوواریانس به صورت متر در کیلوگرم در نظر گرفته می‌شود.
- کوواریانس بین X و X با واریانس برابر خواهد بود. COV(X,X) = (V(X)
- اگر رابطه‌ای خطی بین X و Y وجود داشته باشد، یعنی داشته باشیم: a + bX = Y، آنگاه COV(X,Y) = bV(X). این بدان معنی است که تغییر مکان داده‌ها بر مقدار کوواریانس تاثیری نداشته و فقط تغییر مقیاس موجب می‌شود که کوواریانس نیز به همان مقیاس تبدیل شود.
- با در نظر گرفتن مقیاس اندازه‌گیری داده‌ها، بزرگی یا کوچکی کوواریانس برای مقایسه مناسب نیست.
مثال
بر اساس مطالعه روی قد و وزن ۹ نوزاد، داده‌های زوجی (x,y) در جدول زیر نشان داده شده‌اند. کوواریانس میان قد و وزن این افراد برابر است با 10.80 کیلوگرم در سانتی‌متر.
میانگین وزن‌ها برابر با 6.6 کیلوگرم و میانگین قدها نیز برابر با 62.4 سانتی‌متر است. محاسبات مورد نیاز برای به دست آوردن کوواریانس نیز در جدول زیر نشان داده شده‌اند.
این مقدار حاکی از آن است که رابطه مستقیمی بین قد و وزن کودکان وجود دارد.
ماتریس کوواریانس
در صورتی که لازم باشد ارتباط بین چندین متغیر محاسبه و نمایش داده شود، از ماتریس کوواریانس استفاده می‌شود. متغیرها در سطرها و ستون‌های این ماتریس قرار گرفته و مقادیر درون ماتریس هم کوواریانس مربوط به متغیر سطر با ستون متناظر آن را نشان می‌دهند. در صورتی که X، Y و Z سه متغیر تصادفی باشند، ماتریس کوواریانس آنها به صورت زیر نشان داده می‌شود:
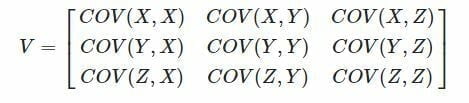
از آنجا که کوواریانس هر متغیر برابر با واریانس آن متغیر است، گاهی به V، ماتریس واریانس-کوواریانس نیز گفته می‌شود. لازم به ذکر است که ماتریس V یک ماتریس متقارن است و عناصر روی قطر اصلی واریانس ها هستند.
محاسبه ضرایب همبستگی
همان طور که پیش از این گفته شد، کوواریانس به واحد اندازه‌گیری داده‌ها بستگی دارد. در نتیجه، نمی‌توانیم بزرگی کوواریانس دو متغیر را با بزرگی کوواریانس دو متغیر دیگر بدون در نظر گرفتن واحد اندازه‌گیری آنها، مقایسه کنیم. ضریب همبستگی که شاخصی بدون واحد است، این مسئله را حل کرده است.
در بخش‌های قبل متوجه شدیم که ضریب همبستگی هم برای اندازه‌گیری میزان وابستگی بین دو متغیر مورد استفاده قرار می‌گیرد. با در نظر گرفتن نوع داده‌ها، روش‌های گوناگونی برای اندازه‌گیری آن وجود دارند. این ضریب اغلب رابطه بین مقادیر میانگین دو متغیر را نشان می‌دهد و معمولاً با ρ و یا r نشان داده می‌شود.
در این مقاله، قصد داریم ضریب همبستگی پیرسون (Pearson Correlation Coefficient)، ضریب همبستگی اسپیرمن (Spearman Correlation Coefficient) و ضریب همبستگی کندال (Kendall Correlation Coefficient) را مورد بررسی قرار داده و شیوه محاسبه آنها را مرور می‌کنیم.
ضریب همبستگی پیرسون
یکی از رایج‌ترین روش‌های اندازه‌گیری وابستگی بین دو متغیر کمّی، محاسبه ضریب همبستگی پیرسون است. این شاخص در سال 1900، توسط کارل پیرسون (Karl Pearson)، کارشناس انگلیسی آمار، در مقاله‌ای معرفی شد. او از این شاخص برای بررسی علمی موضوعات مختلف مربوط به علوم زیستی و حتی جمعیتی استفاده کرد و به نتایج قابل توجهی رسید. در ادامه، روش محاسبه این ضریب ذکر می‌شود.
محاسبه ضریب همبستگی پیرسون
این روش میان دو متغیر تصادفی برابر با کوواریانس آنها تقسیم بر انحراف معیار آنها تعریف می‌شود.
در مورد یک جامعهٔ آماری، ضریب همبستگی جامعه به صورت زیر تعریف می‌شود:
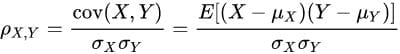
که در این معادله، cov کوواریانس، σx انحراف معیار متغیر X، µx میانگین متغیر X و E امید ریاضی است. منظور از امید ریاضی مقدارِ قابل انتظاری از یک متغیر تصادفیِ گسسته است که برابر است با مجموع حاصل‌ضرب احتمالِ وقوع هر یک از حالات ممکن در مقدار آن حالت.
برای یک نمونه آماری با n زوج داده (Xi, Yi)، ضریب همبستگی پیرسون به صورت زیر تعریف می‌شود:
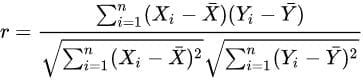
فرمول زیر نیز معادل تعریف فوق است:
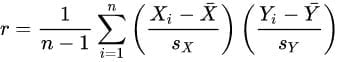
که در آن، کمیت‌ها به شکل زیر تعریف شده‌اند:
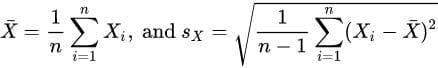
همان طور که پیش از این گفته شد، ضریب همبستگی پیرسون بین -1 و 1 تغییر می‌کند. اگر r=1 باشد، نشان دهنده رابطه مستقیم کامل بین دو متغیر است. رابطه مستقیم یا مثبت نشان می‌دهد که اگر یکی از متغیرها افزایش (کاهش) یابد، دیگری نیز افزایش (کاهش) می‌یابد.
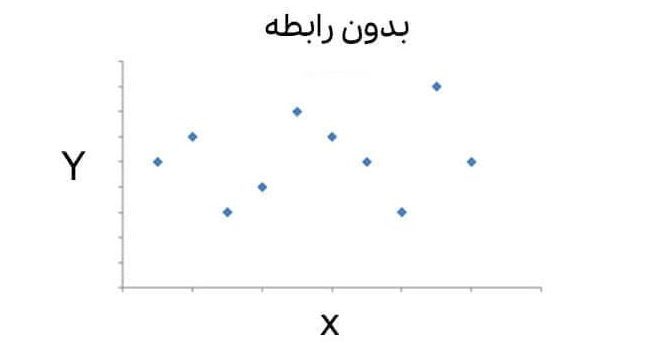
در صورتی که r= -1 باشد، آن گاه رابطه معکوس کاملی بین دو متغیر وجود دارد. رابطه معکوس یا منفی حاکی از آن است که اگر یک متغیر افزایش یابد، متغیر دیگر کاهش می‌یابد و بر عکس.
زمانی که ضریب برابر صفر باشد، حاکی از آن است که بین دو متغیر رابطه خطی وجود ندارد.
خصوصیات ضریب همبستگی پیرسون
با توجه به تعریف Pearson correlation coefficient، می‌توانیم به خصوصیات زیر برای آن اشاره کنیم:
- بدون واحد بودن: این ضریب به واحد اندازه‌گیری داده‌ها بستگی ندارد. به عبارت دیگر، این ضریب شاخصی بدون واحد است. گاهی اوقات، حتی آن را به صورت درصدی نیز نشان می‌دهند.
- تقارن ضریب همبستگی پیرسون: روشن است که این روش دارای تقارن است چون COV(X,Y) = COV(Y,X).
- اندازه‌گیری ارتباط خطی بین دو متغیر: هر چه مقدار ضریب همبستگی به ۱ یا ۱- نزدیک‌تر شود، وجود رابطه خطی بین دو متغیر بیشتر می‌شود. فرض کنید a+bX = Y، آنگاه ضریب همبستگی بین X , Y به صورت زیر محاسبه می‌شود:
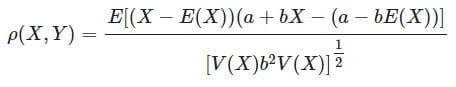
اکنون، تلاش می‌کنیم تا صورت کسر ضریب همبستگی را ساده کنیم:
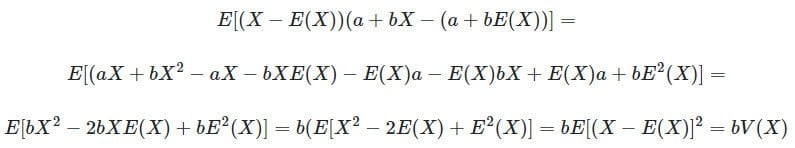
از سوی دیگر، برای واریانس داریم:
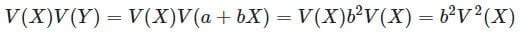
در نتیجه، برای ضریب همبستگی بین X و Y، خواهیم داشت:
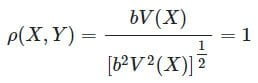
البته، همین محاسبات را برای a-bX=Y نیز می‌توانیم انجام دهیم و نتیجه بگیریم که ضریب همبستگی پیرسون برای چنین رابطه خطی، برابر با ۱- است.
- تعیین جهت همبستگی: در صورتی که این ضریب مثبت باشد، رابطه بین دو متغیر مستقیم و اگر منفی باشد، رابطه بین دو متغیر معکوس خواهد بود.
- استقلال دو متغیر: در صورتی که دو متغیر مستقل از یکدیگر باشند، ضریب همبستگی پیرسون برابر با صفر خواهد بود. البته عکس این قضیه صادق نیست. یعنی این ضریب ممکن است برای دو متغیر برابر با صفر باشد، در حالی که آن دو متغیر مستقل از یکدیگر نیستند.
در این حالت، اگر X یک متغیر تصادفی متقارن حول صفر باشد، یعنی E(X) = E(X3) = 0 و متغیر تصادفی y به صورت Y = X2 باشد، آن گاه ضریب همبستگی بین آنها برابر با صفر است اما روشن است که Y کاملا به X وابسته است. پس محاسبه ضریب همبستگی پیرسون به صورت زیر خواهد بود:
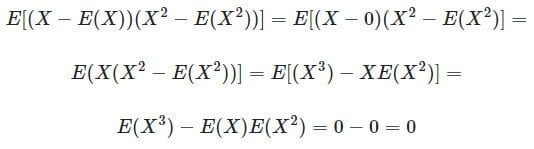
به این ترتیب، برای دو متغیر X و Y که به شدت به هم مرتبط هستند، ضریب برابر با صفر خواهد بود.
- استقلال برای دو متغیر نرمال: اگر دو متغیر X و Y توزیع نرمال داشته باشند، آن گاه صفر بودن ضریب همبستگی می‌تواند دلیلی برای استقلال دو متغیر تصادفی نرمال باشد.
- ضریب همبستگی نمونه‌ای: اگر نمونه‌ای تصادفی با حجم n از متغیرهای تصادفی X و Y به صورت (xi, yi) داشته باشیم، ضریب همبستگی پیرسون به صورت زیر محاسبه خواهد شد:
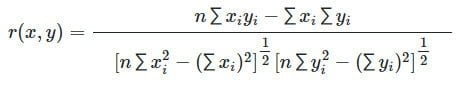
ضریب همبستگی رتبه‌ای اسپیرمن
با توجه به این که ضریب پیرسون بر اساس میانگین و واریانس محاسبه می‌گردد، ممکن است در مقابل داده‌های دورافتاده، منحرف شده و میزان همبستگی را به درستی نشان ندهد. در چنین حالتی، ضریب همبستگی رتبه‌ای اسپیرمن مورد استفاده قرار می‌گیرد.
مانند ضریب پیرسون، ضریب همبستگی رتبه‌ای اسپیرمن میزان تمایل یک متغیر به پیروی کردن از مقدارهای متغیر دیگر را نشان می‌دهد. این شاخص همبستگی برای اولین بار، در سال 1904 توسط چارلز اسپیرمن (Charles Spearman)، دانشمند روانشناس انگلیسی، معرفی شد. او با استفاده از این شیوه توانست نظریه‌های خود در مورد شناخت و هوش را توسعه دهد.
در این نوع ضریب، به جای محاسبه روی مقدارها، از رتبه‌ها استفاده می‌شود. به همین خاطر است که به آن ضریب همبستگی رتبه‌ای گفته می‌شود. به این ترتیب، اگر rx1, rx2, …, rxn رتبه‌های مربوط به مقادیر x1, x2, …, xn و ry1, ry2, …, ryn رتبه‌های مربوط به مقادیر y1, y2, …, yn باشد، ضریب همبستگی رتبه‌ای اسپیرمن که به شکل rs نمایش داده می‌شود، مطابق با رابطه زیر محاسبه می‌شود:
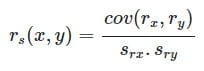
روشن است که در ضریب همبستگی رتبه‌ای اسپیرمن، مبنای محاسبه رتبه‌ها هستند، نه خود مقدارها. علاوه بر این، ضریب اسپیرمن شدت رابطه خطی را ارزیابی نمی‌کند. به عبارت دیگر، ممکن است این ضریب برابر با ۱ باشد در حالی که رابطه خطی بین دو متغیر وجود نداشته باشد.
مثال
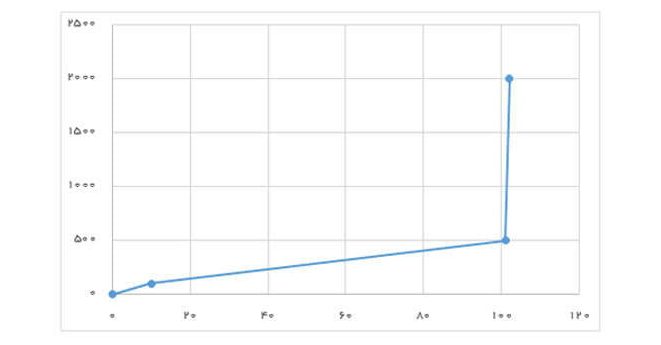
برای داده‌های دوتایی (102,2000)، (101,500)، (10,100) و (0,1)، مقدار ضریب همبستگی اسپیرمن برابر با ۱ است، در حالی که نمودار ترسیمی رابطه خطی را نشان نمی‌دهد و ضریب همبستگی پیرسون برابر با 0.754 است.
ضریب هماهنگی کندال
مانند ضریب همبستگی اسپیرمن، ضریب هماهنگی کندال نیز به جای مقدار از ترتیب مقدارها برای اندازه‌گیری میزان وابستگی استفاده می‌کند. این شاخص برای اولین بار در سال 1938، توسط موریس کندال (Maurice Kendall)، دانشمند انگلیسی علم آمار معرفی شد. به وسیله این شاخص، او میزان همخوانی رتبه‌ها را ارزیابی نمود.
فرض کنید زوج‌های (yn، xn)، … ، (y2، x2)، (y1، x1) مشاهدات متغیرهای X و Y هستند. زوج (yi، xi) و (yj، xj) هماهنگ (Concordant) هستند، یعنی اگر xi < xj باشد، آن گاه yi < yj خواهد بود. به عبارت دیگر، در صورتی که داده‌های این زوج‌ها را بر اساس مولفه اول یا دوم مرتب کنیم، رتبه‌های یکسانی خواهند داشت. در حالت عکس، این زوج‌ها ناهماهنگ (Discordant) نامیده می‌شوند.
اکنون، بر اساس تعریف هماهنگ و ناهماهنگ که برای زوج‌ها ارائه شد، اگر تعداد زوج‌های هماهنگ و ناهماهنگ را به ترتیب، با |Con| و |Dis| نشان دهیم، ضریب هماهنگی کندال به صورت زیر محاسبه می‌شود:
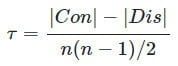
خصوصیات ضریب هماهنگی کندال
- از آنجا که مخرج این کسر نشان دهنده تعداد انتخاب‌های زوج‌ها از بین n مشاهده است، همیشه بزرگتر از صورت است. بنابراین، ضریب همبستگی کندال از ۱ کوچکتر و از ۱- بزرگتر است.
- در صورتی که تمام زوج‌ها با هم هماهنگ باشند، مقدار ضریب هماهنگی کندال برابر با 1 است.
- در صورتی که تمام زوج‌ها ناهماهنگ باشند، مقدار ضریب هماهنگی کندال برابر با 1- است.
- در صورتی که X و Y مستقل باشند، ضریب هماهنگی کندال نیز برابر با صفر خواهد بود.
شکل دیگری هم برای محاسبه ضریب هماهنگی کندال وجود دارد که از تابع علامت یا sgn استفاده می‌کند. منظور از sgn(x) همان علامت x است. در صورتی که علامت x مثبت باشد، sgn برابر با 1 و در صورتی که منفی باشد، sgn برابر با 1- خواهد بود. در صورتی که x برابر با صفر باشد، مقدار sgn صفر خواهد بود. بنابراین، ضریب هماهنگی کندال به صورت زیر محاسبه می‌شود:
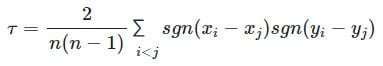
مثال
محاسبات مربوط به ضریب همبستگی اسپیرمن و کندال برای داده‌های مثال ۱ در جدول زیر آورده شده است:
به عنوان مثال، زوج (1،1) نسبت به تمام زوج‌های دیگر هماهنگ است. بنابراین، میزان هماهنگی این زوج برابر با 8 و برای زوج دوم، 7 است. در نتیجه، مجموع تعداد هماهنگی‌ها برابر ۳۶ است.
سخن پایانی
«ضریب همبستگی چیست ؟» در این مقاله به بررسی روش‌های مختلف محاسبه ضریب همبستگی یا ارتباط بین دو متغیر تصادفی پرداختیم. به عنوان یک شاخص مهم، ضریب همبستگی و کوواریانس در این روش‌ها مورد توجه قرار می‌گیرند. همچنین، خصوصیات و ویژگی‌های این دو شاخص نیز مورد بررسی قرار گرفت.
در ادامه، به محاسبه ماتریس کوواریانس و کاربرد آن در بررسی ارتباط بین چندین متغیر پرداختیم. در نهایت، ضریب همبستگی پیرسون به عنوان یک شاخص بدون واحد برای اندازه‌گیری ارتباط بین دو متغیر معرفی شد و محاسبه آن را تشریح کردیم. امیدوارم که این مقاله به شما در درک بهتر وابستگی و ارتباط بین متغیرهای تصادفی کمک کرده باشد.
سئوالات متداول
ضریب همبستگی چیست ؟
ضریب همبستگی یک عدد واحد است که قدرت و جهت رابطه بین متغیرها را توصیف می کند. انواع مختلف ضرایب همبستگی ممکن است برای داده ها بر اساس سطوح اندازه گیری و توزیع آنها مناسب باشد. ضریب همبستگی پیرسون معمولاً برای ارزیابی رابطه خطی بین دو متغیر کمی استفاده می شود.
علامت و مقدار ضریب همبستگی چه چیزی را نشان می دهد؟
این ضرایب همیشه بین 1- و 1 هستند و علامت ضریب جهت رابطه را به شما نشان می دهد. مقدار مثبت به این معنی است که متغیرها با هم در یک جهت تغییر می کنند، در حالی که مقدار منفی به این معنی است که آنها با هم در جهت مخالف تغییر می کنند. بزرگی قدر مطلق یک ضریب همبستگی به معنای همبستگی قوی تر است.
انواع ضریب همبستگی کدامند؟
ضریب همبستگی پیرسون (Pearson Correlation Coefficient)، اسپیرمن (Spearman Correlation Coefficient) و کندال (Kendall Correlation Coefficient).
